Inhaltsverzeichnis
Daten vorbereiten
Die Daten werden zunächst von Excel in eine .csv-Datei
- some.csv
,"Subjective fixation disparity","Dynamic asymmetry","Heterophoria","Nonius bias",,"Subjective baseline","Dynamic asymmetry","Heterophoria","Nonius bias" "AS",-3.28,0.002,-0.68,-0.15,,-2.33,0.002,-0.68,-0.15 "AW",-4.02,0.028,-0.88,-2.67,,-3.13,0.028,-0.88,-2.67 "EE",-4.34,0.004,-1.46,-1.09,,-3.73,0.004,-1.46,-1.09 "IG",1.63,0.058,0.35,-1.3,,2.56,0.058,0.35,-1.3 "JK",-0.54,0.074,0.12,-2.04,,2.37,0.074,0.12,-2.04 "KA",1.06,0.051,-0.12,-1.17,,2.18,0.051,-0.12,-1.17 "KC",0.7,0.052,0.38,1.18,,2.23,0.052,0.38,1.18 "KS",3.69,0.046,0.04,0.18,,6.63,0.046,0.04,0.18 "KT",-2.5,-0.147,-0.4,-1.93,,-2.79,-0.147,-0.4,-1.93 "LF",1.22,-0.019,-0.64,1.44,,-1.01,-0.019,-0.64,1.44 "MW",-1.86,0.035,-1.97,7.22,,4.52,0.035,-1.97,7.22 "NS",2.58,0.031,0.07,1.98,,3.94,0.031,0.07,1.98 "PS",-3.13,-0.023,-0.61,-0.15,,-4.12,-0.023,-0.61,-0.15 "SA",4.67,0.069,-0.3,2.79,,4.35,0.069,-0.3,2.79 "SG",-3.53,-0.12,-1.36,-2.46,,-1.98,-0.12,-1.36,-2.46 "SK",3.62,-0.025,0.09,3.73,,5.07,-0.025,0.09,3.73 "SP",-1.54,-0.073,-0.31,-1.85,,-1.25,-0.073,-0.31,-1.85 "SR",-3.22,-0.049,-1.06,0.04,,-1.72,-0.049,-1.06,0.04 "TB",-1.34,0.1,-3.8,-0.38,,-2.59,0.1,-3.8,-0.38 "WM",-2.72,0.033,-0.33,-0.33,,-0.67,0.033,-0.33,-0.33
gespeichert.
Diese Datei läßt sich in einen Dataframe aiga.some nach R einlesen mit:
aiga.some <- read.csv("some.csv")
Lange Variablennamen machen Verdruß, also ersetzen wir sie durch kürzere (kann man auch besser schon vorher machen), außerdem wählen wir nur die Spalten 1-5 und 7 aus:
colnames(aiga.some) <- c("VP","sFD","dynAsym","HPh","NF","X.1","sBaseL")
aiga.some <- aiga.some[c(1:5,7)]
Aus der größeren Tabelle aiga2 externe Datei übernehmen wir die Dunkelvergenz:
aiga2 <- read.table("aiga2.dat")
aiga.some$DV <- aiga2$DV
Das geht natürlich nur, wenn die Tabellen dieselbe Reihenfolge der Zeilen (=VPs) haben.
Damit bleibt übrig:
> aiga.some VP sFD dynAsym HPh NF sBaseL DV 1 AS -3.28 0.002 -0.68 -0.15 -2.33 0.77 2 AW -4.02 0.028 -0.88 -2.67 -3.13 0.96 3 EE -4.34 0.004 -1.46 -1.09 -3.73 0.54 4 IG 1.63 0.058 0.35 -1.30 2.56 1.11 5 JK -0.54 0.074 0.12 -2.04 2.37 0.73 6 KA 1.06 0.051 -0.12 -1.17 2.18 0.88 7 KC 0.70 0.052 0.38 1.18 2.23 1.38 8 KS 3.69 0.046 0.04 0.18 6.63 0.69 9 KT -2.50 -0.147 -0.40 -1.93 -2.79 0.85 10 LF 1.22 -0.019 -0.64 1.44 -1.01 0.84 11 MW -1.86 0.035 -1.97 7.22 4.52 0.33 12 NS 2.58 0.031 0.07 1.98 3.94 1.10 13 PS -3.13 -0.023 -0.61 -0.15 -4.12 0.80 14 SA 4.67 0.069 -0.30 2.79 4.35 0.81 15 SG -3.53 -0.120 -1.36 -2.46 -1.98 1.00 16 SK 3.62 -0.025 0.09 3.73 5.07 1.45 17 SP -1.54 -0.073 -0.31 -1.85 -1.25 0.91 18 SR -3.22 -0.049 -1.06 0.04 -1.72 0.40 19 TB -1.34 0.100 -3.80 -0.38 -2.59 0.71 20 WM -2.72 0.033 -0.33 -0.33 -0.67 0.30 >
Regression (lineares Modell)
Wir wissen zwar schon, daß der Datensatz Probleme haben wird bzgl. der statistischen Robustheit, aber vorerst gehen wir darauf noch nicht ein.
Eine lineare Regression ohne Interaktionsterme kann man jetzt durchführen und in
einem Objekt sFD.lm zwischenspeichern mit
sFD.lm <- lm(sFD ~ dynAsym + HPh + NF,aiga.some)
Die wichtigsten Informationen über ein Objekt erfährt man mit der Funktion summary. Für die Regression sind das die Residuen (Abweichungen von der Regressionsgleichung), sowie die Estimates für die Koeffizienten und die t-Werte.
> summary( sFD.lm )
Call:
lm(formula = sFD ~ dynAsym + HPh + NF, data = aiga.some)
Residuals:
Min 1Q Median 3Q Max
-2.846 -1.913 0.681 1.301 2.869
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.152 0.573 0.27 0.7936
dynAsym 14.518 7.751 1.87 0.0794 .
HPh 1.485 0.501 2.96 0.0092 **
NF 0.450 0.209 2.15 0.0467 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.12 on 16 degrees of freedom
Multiple R-squared: 0.531, Adjusted R-squared: 0.443
F-statistic: 6.03 on 3 and 16 DF, p-value: 0.00598
>
Das Zwischenspeichern ist bei einfachen Designs überflüssig, man kann sich auch gleich das Ergebnis ansehen mit
summary(lm(sFD~dynAsym+HPh+NF,aiga.some))
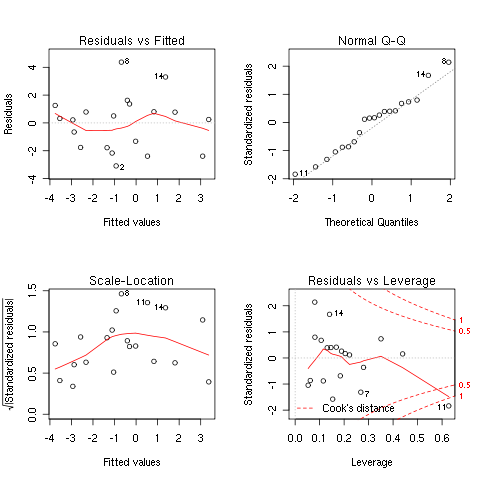
Leider haben wir keinen Hinweis darauf bekommen, daß das Ergebnis problematisch ist. Den gibt es erst, wenn man die diagnostischen Plots anfordert:
plot(lm(sFD~dynAsym+HPh+NF,aiga.some))
Es kommen jetzt 4 Plots, vor allem im vierten davon wird klar, daß die Zeilen 11 und 19 untypische Daten enthalten.
Variationen
1. weitere Terme in der Formel
Um alle möglichen Interaktionsterme zu erzeugen, verwendet man * statt +:
> summary(lm(sFD ~ dynAsym * HPh * NF , aiga.some))
Call:
lm(formula = sFD ~ dynAsym * HPh * NF, data = aiga.some)
Residuals:
Min 1Q Median 3Q Max
-2.6083 -0.8351 0.0281 1.1093 2.6128
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.675 0.633 1.07 0.307
dynAsym 6.894 11.446 0.60 0.558
HPh 3.121 0.960 3.25 0.007 **
NF 0.819 0.286 2.87 0.014 *
dynAsym:HPh -25.091 12.611 -1.99 0.070 .
dynAsym:NF 1.954 5.672 0.34 0.737
HPh:NF 0.639 0.265 2.41 0.033 *
dynAsym:HPh:NF -9.765 7.588 -1.29 0.222
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.79 on 12 degrees of freedom
Multiple R-squared: 0.748, Adjusted R-squared: 0.601
F-statistic: 5.08 on 7 and 12 DF, p-value: 0.007
>
Will man nur einige Interaktionen aussuchen, kann man das auch explizit hinschreiben:
lm(sFD ~ dynAsym + HPh + NF + dynAsym:HPh + dynAsym:NF + HPh:NF + dynAsym:HPh:NF, aiga.some)
Immerhin wird das Problem jetzt manifest: die Estimates für die Terme dynAsym und HPh haben sich massiv verändert, und es ist nicht mehr dynAsym als 7%-signifikant bezeichnet, sondern nur noch die Interaktion dynAsym:HPh.
2. robuste Regression statt einfaches lineares Modell:
> summary(rlm(sFD ~ dynAsym + HPh + NF,aiga.some))
Call: rlm(formula = sFD ~ dynAsym + HPh + NF, data = aiga.some)
Residuals:
Min 1Q Median 3Q Max
-2.846 -1.913 0.681 1.301 2.869
Coefficients:
Value Std. Error t value
(Intercept) 0.152 0.573 0.266
dynAsym 14.518 7.751 1.873
HPh 1.485 0.501 2.962
NF 0.450 0.209 2.155
Residual standard error: 2.62 on 16 degrees of freedom
>
Es werden keine p-Werte angegeben. Diese würden nur unter der Annahme normalverteilter Fehler gelten. Robuste Statistik macht man aber, weil man diese Voraussetzung in Frage stellt. Ansonsten hat das robuste Verfahren das Problem nicht gelöst. Das Ergebnis ist praktisch dasselbe wie vorher. Warum das so ist, wird weiter unten zu erörtern sein.
3. Weglassen einzelner VPs (TB ist No. 19):
> summary(lm(sFD ~ dynAsym + HPh + NF,subset(aiga.some, VP != "TB")))
Call:
lm(formula = sFD ~ dynAsym + HPh + NF, data = subset(aiga.some,
VP != "TB"))
Residuals:
Min 1Q Median 3Q Max
-2.3359 -0.7545 -0.0473 0.7933 2.8864
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.860 0.500 1.72 0.10578
dynAsym 1.893 7.208 0.26 0.79645
HPh 3.317 0.683 4.86 0.00021 ***
NF 0.641 0.174 3.68 0.00225 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.67 on 15 degrees of freedom
Multiple R-squared: 0.727, Adjusted R-squared: 0.672
F-statistic: 13.3 on 3 and 15 DF, p-value: 0.000169
>
Die Signifikanz von dynAsym ist nicht mehr vorhanden. Die Estimates haben auch stark veränderte Werte.
Damit ist gezeigt, daß die Estimates aus der ursprünglichen Auswertung an einem Einzelfall hängen. Sie können, selbst wenn sie richtig wären, nicht mit Mitteln der Statistik gestützt werden.
Statt subset(aiga.some, VP != „TB“) hätte man auch schreiben können: aiga.some[-19,] (Datensatz ohne Zeile 19),
was bei mehreren Ausschlußbedingungen zu kürzeren Formulierungen führt, zB. aiga.some[-c(11,19),], wenn man auch Zeile 11 weglassen möchte.
robuste Korrelationen
Wir betrachten jetzt die Korrelationen der Variablen. Zunächst einmal der Test eines einzelnen Paars:
> cor.test(~ HPh + dynAsym, aiga.some) Pearson's product-moment correlation data: HPh and dynAsym t = -0.225, df = 18, p-value = 0.8243 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.484 0.399 sample estimates: cor -0.053 >
Demnach wären HPh und dynAsym unkorreliert.
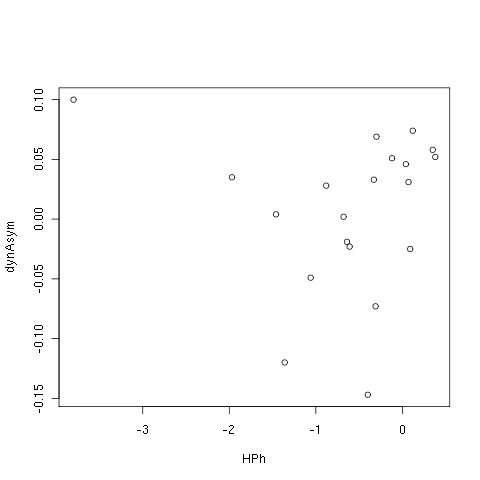
Das Datenpaar kann man auch plotten:
plot(~ HPh + dynAsym, aiga.some)
Der Punkt links oben sieht nach einem möglichen Ausreißer aus.
Das Ergebnis ist nicht robust, da ohne Z. 11 und 19 eine signifikant positive Korrelation entsteht:
> cor.test(~ HPh + dynAsym, aiga.some[-c(19,11),]) Pearson's product-moment correlation data: HPh and dynAsym t = 2.35, df = 16, p-value = 0.03171 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: 0.0527 0.7875 sample estimates: cor 0.507 >
Wir laden (falls nicht schon geschehen) das Funktionspaket robust:
library(robust)
suchen dann mit „fuzzy search“ nach correlation
?? correlation
wobei uns u.a. angeboten wird:
...
pls::scoreplot Plots of Scores, Loadings and Correlation
Loadings
robust::covRob Robust Covariance/Correlation Matrix Estimation
stats::acf Auto- and Cross- Covariance and -Correlation
...
und berechnen den Korrelationskoffizienten der Spalten 3 und 4 mit einem robusten Verfahren. Näheres über die Funktion erfährt man mit
? covRob
covRob package:robust R Documentation
Robust Covariance/Correlation Matrix Estimation
Description:
Compute robust estimates of multivariate location and scatter.
Usage:
covRob(data, corr = FALSE, distance = TRUE, na.action = na.fail,
estim = "auto", control = covRob.control(estim, ...), ...)
Arguments:
data: a numeric matrix or data frame containing the data.
corr: a logical flag. If 'corr = TRUE' then the estimated
correlation matrix is computed.
...
oder http://www.uni-koeln.de/rrzk/kurse/unterlagen/s/library/robust/html/covRob.html.
> covRob(aiga.some[,c(3,4)],corr=T)
Call:
covRob(data = aiga.some[, c(3, 4)], corr = T)
Robust Estimate of Correlation:
dynAsym HPh
dynAsym 1.000 0.592
HPh 0.592 1.000
Robust Estimate of Location:
dynAsym HPh
0.0207 -0.3194
>
Im Lehrbuch „Robust Statistics“ von Maronna et al. (Inst.-Bibl. A II 174) werden auf p. 204f die Probleme der „pairwise robust covariance“ diskutiert, die dadurch entstehen, daß bei einem Datensatz mit mehr als 2 Variablen bei jeder paarweisen Korrelation die jeweiligen Ausreißer völlig andere Beobachtungen sein können. Daher sollte man die Korrelationsmatrix besser als Ganzes (ich wähle die Spalten 2:5 aus, entsprechend den Variablen in der Regression oben) robust berechnen:
> covRob(aiga.some[,2:5],corr=T)
Call:
covRob(data = aiga.some[, 2:5], corr = T)
Robust Estimate of Correlation:
sFD dynAsym HPh NF
sFD 1.000 0.482 0.772 0.483
dynAsym 0.482 1.000 0.744 -0.291
HPh 0.772 0.744 1.000 0.237
NF 0.483 -0.291 0.237 1.000
Robust Estimate of Location:
sFD dynAsym HPh NF
-0.7868 0.0212 -0.3799 -0.2538
>
Unter diesen Bedingungen wird die Korrelation zwischen dynAsym und HPh auf 0.74 geschätzt!
Der wesentliche Unterschied zwischen dieser Betrachtung der Daten und der Regressionsrechnung ist, daß bei der Korrelation alle Variablen gleich behandelt werden, wogegen bei der Regression die unabhängigen Variablen nicht in die Ausreißerbehandlung einbezogen werden. Dies ist der Grund, warum oben die Anwendung einer robusten Regression keine Verbesserung liefert; denn die Besonderheit der Werte in Z. 19 ist daß gleichzeitig ein Maximalwert von HPh und Minimalwert von dynAsym vorliegt (beides unabh. Variablen der Regression), während der sFD-Wert unauffällig ist.
Z. Vergleich die klassische Korrelationsmatrix
> ccov(aiga.some[,2:5],corr=T)
Call:
ccov(data = aiga.some[, 2:5], corr = T)
Classical Estimate of Correlation:
sFD dynAsym HPh NF
sFD 1.000 0.400 0.4627 0.4265
dynAsym 0.400 1.000 -0.0530 0.2495
HPh 0.463 -0.053 1.0000 -0.0748
NF 0.426 0.249 -0.0748 1.0000
Classical Estimate of Location:
sFD dynAsym HPh NF
-0.64250 0.00635 -0.64350 0.15200
>
mit dem Wert von -0.053 wie im ersten Korrelationstest zwischen dynAsym und HPh.
Einzelfälle
Z.19
Der Fall TB in Z. 19 wurde bereits andiskutiert. Auffällig ist hier eigentlich nur die HPh-Messung, die dazu führt, daß die Gesamtheit der HPh-Werte nicht normalverteilt ist:
> shapiro.test(aiga.some$HPh[-19]) Shapiro-Wilk normality test data: aiga.some$HPh[-19] W = 0.943, p-value = 0.2932 > shapiro.test(aiga.some$HPh) Shapiro-Wilk normality test data: aiga.some$HPh W = 0.822, p-value = 0.001889 >
Bei der HPh-Messung handelt es sich offenbar nicht um einen Meßfehler, da dieselbe VP auch in anderen – völlig unabhängigen – Versuchen konsistent ähnliche Werte produziert hat. Es wäre allerdings noch nachzuprüfen, ob eine Messung der Heterophorie mit üblichen optometrischen Verfahren dasselbe Ergebnis liefert wie die Messung in der monokularen Kalibration.
Eine naheliegende Frage ist, ob es weitere Fälle gibt, daß eine Variable durch einen Einzelfall signifikant nichtnormal wird. Dies ist der Fall:
Z. 11
> shapiro.test(aiga.some$NF) Shapiro-Wilk normality test data: aiga.some$NF W = 0.881, p-value = 0.01875 > shapiro.test(aiga.some$NF[-11]) Shapiro-Wilk normality test data: aiga.some$NF[-11] W = 0.946, p-value = 0.3424 >
zeigt, daß der Ausreißer von VP MW in Z. 11 ebenfalls unter Beobachtung bleiben muß, hier wegen des ungewöhnlich großen Noniusfehlers, der hier zwar auch an den beiden anderen Meßtagen gefunden wurde, aber für den keine Messungen aus anderen Versuchen vorlagen. Unabhängig davon, ob sich der Verdacht auf einen Meßfehler erhärtet, sollte man zur Verkleinerung der Leverage (Hebel-Effekt) für die Regression die Standardabeichung unabhängiger Variablen auf den Ein-Sigma-Bereich verkleinern, zB indem man den Meßwert der Ausreißer auf das Maximum der übrigen Messungen vermindert. Dieser Vorschlag hätte im Fall der HPh bei TB nicht ausgereicht, da dort die Gegenläufigkeit von dynAsym un HPh im Gegensatz zu den übrigen Datensätzen das Hauptproblem darstellte.
Dunkelvergenz
Im folgenden soll versucht werden, die Regression statt HPh mit der Dunkelvergenz DV durchzuführen, die in der Regel und auch in desem Datensatz positiv mit der Heterophorie korreliert. Die Messungen sind normalverteilt:
> shapiro.test(aiga.some$DV) Shapiro-Wilk normality test data: aiga.some$DV W = 0.962, p-value = 0.5881 >
Wir beginnen diesmal mit der robusten Korrelation:
> summary(covRob(aiga.some[,c(2,3,5,7)],corr=T))
Call:
covRob(data = aiga.some[, c(2, 3, 5, 7)], corr = T)
Robust Estimate of Correlation:
sFD dynAsym NF DV
sFD 1.000 0.446 0.6101 0.5356
dynAsym 0.446 1.000 -0.1240 0.2798
NF 0.610 -0.124 1.0000 0.0606
DV 0.536 0.280 0.0606 1.0000
Robust Estimate of Location:
sFD dynAsym NF DV
-0.8991 0.0262 -0.2563 0.7666
Eigenvalues:
Eval. 1 Eval. 2 Eval. 3 Eval. 4
2.003 1.187 0.689 0.121
Robust Distances:
[1] 1.66 3.10 1.18 2.69 2.47 1.93 10.45 6.55 24.85 2.12 48.56 3.04
[13] 1.66 4.19 17.86 13.78 11.10 3.52 4.30 3.20
>
Die Korrelation der sFD mit den übrigen drei Variablen ist größer als die Korrelationen innerhalb der anderen Variablen, so daß, mit Ausnahme der VP MW in Z. 11 möglicherweise eine günstigere Voraussetzung für eine erfolgreiche Regression besteht.
> summary(lm(sFD~NF+DV+dynAsym,aiga.some))
Call:
lm(formula = sFD ~ NF + DV + dynAsym, data = aiga.some)
Residuals:
Min 1Q Median 3Q Max
-3.093 -1.769 0.282 0.916 4.373
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.700 1.428 -3.29 0.0046 **
NF 0.436 0.210 2.08 0.0542 .
DV 4.705 1.619 2.91 0.0103 *
dynAsym 15.057 7.812 1.93 0.0719 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.13 on 16 degrees of freedom
Multiple R-squared: 0.525, Adjusted R-squared: 0.435
F-statistic: 5.88 on 3 and 16 DF, p-value: 0.00662
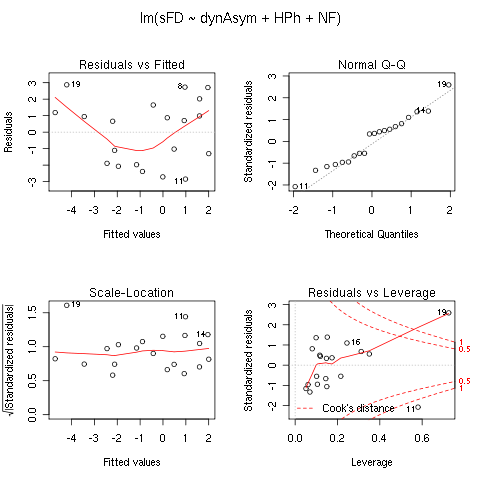
Zur Kontrolle machen wir den diagnostischen Plots:
Erwartungsgemäß hat der Ausreißer von Z.11 eine deutlich zu große Leverage. Ohne diese Zeile erhalten wir robustere Werte, allerdings ist die Veränderung bei weitem nicht so groß wie in der ursprünglichen Auswertung mit HPh als unabhängiger Variable.
> summary(lm(sFD~NF+DV+dynAsym,aiga.some[-11,]))
Call:
lm(formula = sFD ~ NF + DV + dynAsym, data = aiga.some[-11, ])
Residuals:
Min 1Q Median 3Q Max
-2.469 -1.699 0.130 1.390 3.893
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.044 1.548 -1.97 0.0681 .
NF 0.851 0.283 3.01 0.0088 **
DV 3.032 1.704 1.78 0.0954 .
dynAsym 12.957 7.241 1.79 0.0938 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.95 on 15 degrees of freedom
Multiple R-squared: 0.621, Adjusted R-squared: 0.545
F-statistic: 8.2 on 3 and 15 DF, p-value: 0.00182
>
Die Variablen DV und dynAsym tragen demnach etwa gleichsignikant bei, während der Koeffizient 0.85 des NF ausreichend nahe bei der theoretisch optimalen 1 liegt, um die Auswertung für die noniusfehlerkorrigierte FD sFD - NF zu wagen:
> summary(lm(sFD-NF~DV+dynAsym,aiga.some[-11,]))
Call:
lm(formula = sFD - NF ~ DV + dynAsym, data = aiga.some[-11, ])
Residuals:
Min 1Q Median 3Q Max
-2.508 -1.449 -0.025 1.519 3.827
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.75 1.41 -1.95 0.069 .
DV 2.73 1.57 1.74 0.101
dynAsym 11.92 6.81 1.75 0.099 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.91 on 16 degrees of freedom
Multiple R-squared: 0.269, Adjusted R-squared: 0.178
F-statistic: 2.94 on 2 and 16 DF, p-value: 0.0815
>
Zum Vergleich berechnen wir die Regression ohne die Noniusfehlerkorrektur:
> summary(lm(sFD~DV+dynAsym,aiga.some[-11,]))
Call:
lm(formula = sFD ~ DV + dynAsym, data = aiga.some[-11, ])
Residuals:
Min 1Q Median 3Q Max
-4.38063 -1.82182 -0.00857 1.23254 4.26976
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.72 1.77 -2.66 0.017 *
DV 4.74 1.97 2.41 0.028 *
dynAsym 18.89 8.55 2.21 0.042 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.4 on 16 degrees of freedom
Multiple R-squared: 0.392, Adjusted R-squared: 0.316
F-statistic: 5.16 on 2 and 16 DF, p-value: 0.0186
>
Anwendung "stepwise search"
Es gibt noch eine elegante Methode in R, um die signifikanten Terme in der Regressionsrechnung zu finden, nämlich die schrittweise Suche nach Verbesserungen des Akaike_information_criterion, ausgehend von einem Modell mit allen möglichen Interaktionen:
> step(lm(sFD~NF*DV*dynAsym,aiga.some[-11,]))
Start: AIC=32.1
sFD ~ NF * DV * dynAsym
Df Sum of Sq RSS AIC
- NF:DV:dynAsym 1 3.5 47.8 31.5
<none> 44.3 32.1
Step: AIC=31.5
sFD ~ NF + DV + dynAsym + NF:DV + NF:dynAsym + DV:dynAsym
Df Sum of Sq RSS AIC
- NF:dynAsym 1 0.1 47.9 29.6
- DV:dynAsym 1 3.6 51.5 30.9
- NF:DV 1 4.1 51.9 31.1
<none> 47.8 31.5
Step: AIC=29.6
sFD ~ NF + DV + dynAsym + NF:DV + DV:dynAsym
Df Sum of Sq RSS AIC
- DV:dynAsym 1 4.3 52.2 29.2
<none> 47.9 29.6
- NF:DV 1 7.9 55.8 30.5
Step: AIC=29.2
sFD ~ NF + DV + dynAsym + NF:DV
Df Sum of Sq RSS AIC
- NF:DV 1 5.0 57.2 29.0
<none> 52.2 29.2
- dynAsym 1 10.0 62.2 30.5
Step: AIC=28.9
sFD ~ NF + DV + dynAsym
Df Sum of Sq RSS AIC
<none> 57.2 29.0
- DV 1 12.1 69.3 30.6
- dynAsym 1 12.2 69.5 30.6
- NF 1 34.6 91.8 35.9
Call:
lm(formula = sFD ~ NF + DV + dynAsym, data = aiga.some[-11, ])
Coefficients:
(Intercept) NF DV dynAsym
-3.044 0.851 3.032 12.957
>
In der Tat minimiert das bereits am Anfang verwendete Modell mit allen Variablen ohne Interaktionen das AIC, die verbliebenen Terme sind also statistisch signifikant.