Vorbemerkung. Die verschiedenen R- und shell-Skripts werden beschrieben wie verwendet im Verzeichnis mifd. Manche Dinge sind obsolet oder nur historisch erklärbar, also bei Neuanlage anders zu machen.

Die Daten kommen aus dem Labor als Zip-Datei mit Versuchskennung, z.B. TB1.ZIP

Archive:  /home/wb/projekt6/mishfd.data/TB1.ZIP
 Length   Method    Size  Cmpr    Date    Time   CRC-32   Name
--------  ------  ------- ---- ---------- ----- --------  ----
    1326  Defl:N      198  85% 10-10-2007 11:06 46ceb64e  MS1SFD03.TB1
 1477940  Defl:N   413435  72% 10-10-2007 11:06 e119e660  MS1MFD03.TB1
    3926  Defl:N      469  88% 10-10-2007 11:13 6696e81e  MS1SFD04.TB1
 2819840  Defl:N   816431  71% 10-10-2007 11:13 af262a3a  MS1MFD04.TB1
    3926  Defl:N      448  89% 10-10-2007 11:21 df50c529  MS1SNF05.TB1
 2824180  Defl:N   802865  72% 10-10-2007 11:21 b5ed3360  MS1MNF05.TB1
    1326  Defl:N      190  86% 10-10-2007 11:26 08da839c  MS1SFD12.TB1
 1400560  Defl:N   381708  73% 10-10-2007 11:26 8f430d1f  MS1MFD12.TB1
    3926  Defl:N      487  88% 10-10-2007 11:33 7d981890  MS1SFD13.TB1
 2792780  Defl:N   797528  72% 10-10-2007 11:33 0103da3e  MS1MFD13.TB1
    3926  Defl:N      458  88% 10-10-2007 11:39 b8aa07f7  MS1SNF14.TB1
 2798460  Defl:N   799433  71% 10-10-2007 11:39 c585be3e  MS1MNF14.TB1
    1326  Defl:N      202  85% 10-10-2007 12:20 87203254  MS2SFD03.TB1
 1363260  Defl:N   387516  72% 10-10-2007 12:20 2abd66bf  MS2MFD03.TB1
    3926  Defl:N      458  88% 10-10-2007 12:26 3a2d45b5  MS2SFD04.TB1
 2805600  Defl:N   822853  71% 10-10-2007 12:26 c69077fd  MS2MFD04.TB1
    3926  Defl:N      460  88% 10-10-2007 12:33 bf962e31  MS2SNF05.TB1
 2802580  Defl:N   809568  71% 10-10-2007 12:33 82dff653  MS2MNF05.TB1
    1326  Defl:N      212  84% 10-10-2007 12:40 1fb61d30  MS2SFD12.TB1
 1423580  Defl:N   371341  74% 10-10-2007 12:40 d2b58d79  MS2MFD12.TB1
    3926  Defl:N      461  88% 10-10-2007 12:46 bf7f6dcf  MS2SFD13.TB1
 2828960  Defl:N   824867  71% 10-10-2007 12:46 207a2fc1  MS2MFD13.TB1
    3926  Defl:N      447  89% 10-10-2007 12:52 4c62f82e  MS2SNF14.TB1
 2751500  Defl:N   817611  70% 10-10-2007 12:52 7748d535  MS2MNF14.TB1
--------          -------  ---                            -------
28125952          8049646  71%                            24 files

Um die Daten mit R verarbeiten zu können, möchten wir diese, je ZIP-Datei in einem Unterverzeichnis, in ASCII konvertiert umspeichern. Jeder der Dateien mit M an der 4. Stelle im Namen enthält die interessierenden Daten im festen Format von 5 16bit-Binärzahlen je Meßzeitpunkt. Dazu verwende ich ein bash-Shellskript

hd.sh

for j in MS?M*.??? ; do
  hexdump -v -e '5/ "%d\t" "\n"' <$j > ${j:9:3}/${j:4:4}.${j:0:3} ;
  done

Das Skript zerlegt den angelieferten Dateinamen in Variable $j und baut aus zB MS2MNF14.TB1 einen neuen Dateinamen TB1/NF14.MS2 auf, in dem die mittels hexdump konvertierte Datei abgelegt wird. Wichtig ist die Option -v, damit gleichlautende Zeilen nicht zusammengefaßt werden.

$ head -5 TB1/NF14.MS2
2090	60	62	12295	13783
0	17346	17290	11032	13651
0	17280	17290	11087	13651
0	17218	17094	11133	13475
0	17156	16899	11178	13299
...

Die 1. Zeile enthält Metainformation (neuerdings die 1. beiden Zeilen), die gesondert zu behandeln ist, die übrigen die Meßdaten in der Reihenfolge tg (Trigger), hl, hr, vl, vr.

Die 1. Stufe der Datenauswertung betrifft die Markierung offensichtlicher Artefakte, Auswertung der Kalibrierungsdaten und Umrechnung in kalibrierte Daten.

mifd_1.R

# MiFD-Auswertung jul 2008
vpos <- c(rep(-c(-2,8,24),each=3,times=2),rep(NA,10)) # 3 Hoehen vert. Eichung aus HUD-Versuch
#hpos <- c(rep(c(-2,1,4),times=3),rep(c(2,-1,-4),times=3) ,rep(NA,10))
hpos <- c( -8+2*1:7, -8+2*1:7, rep(NA,16),0) # 7 Pkt horiz. Eichung

Die Vektoren vpos bzw. hpos enthalten die Sollpositionen für die verschiedenen Triggercodes bzw. NA für unbekannte Positionen. In diesem Fall ist vpos irrelevant, da in diesem Versuch nur horizontal geeicht wurde. Besser wäre die Konstruktion dieser Daten und anderer manifester Konstanten aus der Metainformation zum Versuch.

Neben den Konstanten und evt. Unterskripts enthält das Skript mifd.R eine Funktion ausw für die eigentliche Bearbeitung und den Aufruf dieser Funktion für alle Dateien:

mifd_2.R

ausw <- function(fn) {
...
}
 
liste <- readLines("files.dat")
for( fn in liste ) try( ausw.liste[[fn]] <- ausw(fn) ) ;
quit("yes")

Hier wird angenommen, daß eine Datei files.dat mit den Namen der zu verarbeitenden Dateinamen vorliegt (die man beispielsweise in der Shell mittels

ls ???/*.MS? > files.dat

erzeugt hat. Die Funktion ausw liefert dann für jede bearbeitete Datei fn verdichtete Daten, die in der Liste ausw.liste gesammelt werden. Außerdem werden die konvertierten Daten innerhalb der Funktion für evtl. Weiterverarbeitung abespeichert. Indem der eigentliche Befehl

ausw.liste[[fn]] <- ausw(fn)

in try( … ) eingeklammert wird, wird bezweckt, daß evt. Fehler nicht zum Abbruch des gesamten Skripts führen. Da die Operation möglicherweise lange dauert und auch nachts ausgeführt werden kann, wird R danach mit dem Aufruf von quit beendet, der Parameter yes sorgt für das automatische Abspeichern des Workspace.

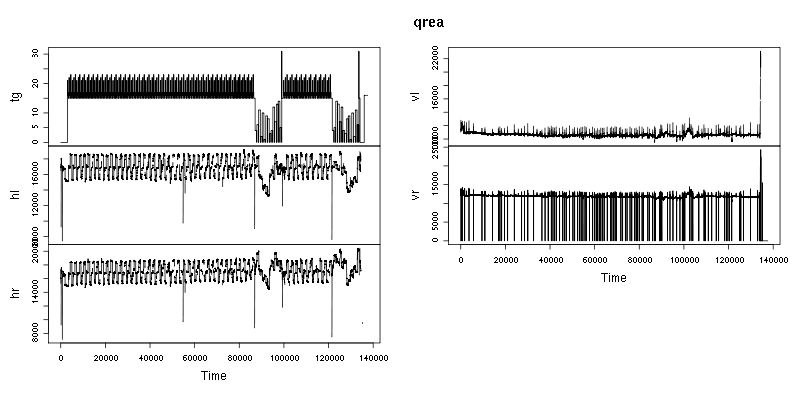
Der 1. Schritt ist das Einlesen der Datei in einen Dataframe qrea (man frage nicht, warum er so heißt) mit Ersetzen der 0 durch NA:

ausw_1.R

qrea <- read.table(fn,skip=1,header=F)
colnames(qrea) <- c("tg","hl","hr","vl","vr")
qrea$hl[qrea$hl==0] <- NA
qrea$hr[qrea$hr==0] <- NA
qrea$vl[qrea$vl==0] <- NA
qrea$vr[qrea$vr==0] <- NA

skip=1 gibt die Anzahl der zu überlesenden Zeilen an, und header=F zeigt an, daß die Eingabedatei keine Spaltennamen enthält.

Bei Neuprogrammierung könnte man schreiben:

qrea <- read.table(fn,skip=1,header=F,na.strings="0",col.names=c("tg","hl","hr","vl","vr") )

Allerdings würden auch die Nullen der tg-Spalte in NA konvertiert, was möglicherweise unerwünscht ist. Man kann sich die eingelesene Datei ansehen mit der Zeitreihen-Plotfunktion plot.ts:

plot.ts(qrea)

Meist ist die Verarbeitung der Trigger günstiger in der Form einer Liste von Triggerzeitpunkten trig und -codes trigv. Um diese zu erzeugen, beginnen wir mit der Liste der Zeiten, an denen sich der Triggercode ändert und entnehmen den neuen Code nach trigv:

ausw_2.R

n <- length(qrea$tg)
trig <- (2:n)[qrea$tg[1:(n-1)] != qrea$tg[2:n]]   # wo sich etwas aendert
trig <- trig[qrea$tg[trig]!=0]                    # triggercode 0 lassen wir aus
trigv <- qrea$tg[trig]
trig <- trig[trigv != c(0,trigv[-length(trigv)])] # durch Entfernen der 0 können Wiederholungen entstanden sein
trigv <- qrea$tg[trig]
stv <- trig[trigv==31]                            # Code 31 markiert Beginn und Ende der Versuchsphase
st <- min(trig[trigv<15][1],2*stv[1]-stv[2])      # wir lassen soviel Daten vor der 1. Eichung wie zwischen den Eichungen
qrea <- qrea[st:stv[2],]                          # der Rest wird vergessen
n <- length(qrea$tg)
trig <- trig[trig>=st]-st+1                       # und die Triggerliste an die neue Länge angepaßt
trigv <- qrea$tg[trig]

Für die Kalibrierung wird der Dataframe qrea um Spalten mit der Zeitzählung tn und um 100 bzw. 200 Abtastungen verschobenen Triggercode erweitert.

ausw_3.R

qrea$tgl <- c(rep(0,100),qrea$tg[1:(length(qrea$tg)-100)]) # Verschiebung um 100 Abtastungen
qrea$tgl2 <- c(rep(0,200),qrea$tg[1:(length(qrea$tg)-200)]) # Verschiebung um 200 Abtastungen
qrea$tn <- 1:n
 
hl.rlm <- rlm( hl ~ I(hpos[tgl])+factor(tn>trig[trigv==31][1]) ,
 subset(qrea,tgl==tgl2&tgl>0&tgl<8),method="MM",init=c(16650,338,0))
hr.rlm <- rlm( hr ~ I(hpos[tgl])+factor(tn>trig[trigv==31][1]) ,
 subset(qrea,tgl==tgl2&tgl>7&tgl<15),method="MM",init=c(14650,338,0))

Die robuste Regression rlm geht von gleicher Verstärkung und möglicherweise unterschiedlichen Intercepts zwischen Vor- und Nachkalibrierung aus, je nachdem ob tn größer oder kleiner als der erste Zeitpunkt mit tg==31 ist. Für die Berechnung der kalibrierten Daten wird der Mittelwert verwendet. Die vertikalen Daten werden umgerechnet mit der doppelten Verstärkung des horizontalen Kanals und ihrem eigenen getrimmten Mittelwert als Intercept.

ausw_4.R

qrea$hl <- (qrea$hl-coef(hl.rlm)[1]) / coef(hl.rlm)[2]
qrea$hr <- (qrea$hr-coef(hr.rlm)[1]) / coef(hr.rlm)[2]
qrea$vl <- 2* (qrea$vl-mean(qrea$vl,trim=0.2,na.rm=T)) / coef(hl.rlm)[2]
qrea$vr <- 2* (qrea$vr-mean(qrea$vr,trim=0.2,na.rm=T)) / coef(hr.rlm)[2]

Abschließend wird der Dataframe etwas aufgeräumt, abgespeichert und die Liste von weiterverwendbaren Ergebnissen zusammengestellt.

ausw_5.R

qrea.nas.orig <- apply(qrea,1,function(x)any(is.na(x)))   # die NA's merken, falls interpoliert wird (hier überflüssig)
 
qrea$tgl <- NULL
qrea$tgl2 <- NULL
qrea$tn <- NULL
 
#plot.ts(qrea,main=fn)
save(qrea,file=paste(fn,".dat",sep=""))
 
qrea.nas <- apply(qrea,1,function(x)any(is.na(x)))         # noch mal NA's merken
 
list(N=n,st=st,coef.hl=coef(hl.rlm),coef.hr=coef(hr.rlm),trig=trig,trigv=trigv,
na.hl=sum(is.na(qrea$hl)),
na.hr=sum(is.na(qrea$hr)),
na.vl=sum(is.na(qrea$vl)),
na.vr=sum(is.na(qrea$vr)),
nas.orig=cbind(beg=(1:length(qrea.nas.orig))[qrea.nas.orig & !c(F,qrea.nas.orig[-length(qrea.nas.orig)])],
  end=(1:length(qrea.nas.orig))[!c(qrea.nas.orig[-1],F) & qrea.nas.orig]),
nas=cbind(beg=(1:length(qrea.nas))[qrea.nas & !c(F,qrea.nas[-length(qrea.nas)])],
  end=(1:length(qrea.nas))[!c(qrea.nas[-1],F) & qrea.nas])
)

Mit dem jetzt vorgestellten Oversampling werden 2 Ziele verfolgt: die Samplingrate wird auf 1000Hz erhöht, die Geschwindigkeiten somit direkt in Grad/ms interpretierbar, außerdem ist die entstehende Zeitreihe ausreichend regulär, so daß man einfach durch Differenzbildung der aufeinander folgenden Werte differenzieren darf.

Trotzdem brauchen wir gelegentlich eine tiefpaßgefilterte Differentiationsroutine. Dazu wird ein Sample der Ableitung der Gaußkurve berechnet:

beta.R

dg <- function(N) {
  step <- 2.5/N
  beta <- (function(x)(x*exp(-x^2)))(step*1:N)
  beta <- c(-beta[N+1-1:N],0,beta)
  beta <- - beta/(1.4*2*pi)*step^2*10
  beta
}

Die Konstanten sind so normiert, daß die Geschwindigkeit direkt durch Anwendung des Filters herauskommt; die Grenzfrequenz ist umgekehrt proportional zur Länge des Filters (müßte ich noch genauer bestimmen). Anwendung auf einen Vektor oz:

dz10 <- filter(oz,dg(10))

maxima.R

require(Hmisc)                       # Farell's Hmisc library
maxima <- function(dh2,limit=0)
  which( dh2 > limit & dh2 < Lag(dh2,1) & dh2 < Lag(dh2,-1) )

Die Funktion dient dazu, alle lokalen Maximalstellen zu finden, die oberhalb von limit liegen. Dazu wird der Vektor mit den um 1 Stelle nach vorn und hinten verschobenen Kopien verglichen.

Die Maxima-Funktion läßt sich auch in Matlab programmieren:

maxima.m

function ret = maxima(dh2,limit=0)
  ret = find(dh2> limit & dh2 > circshift(dh2,1) & dh2 > circshift(dh2,-1) )
  endfunction

ip.R

ip <- function(z) approxfun(1:length(z),z,rule=2)(1:length(z))

NAs werden linear interpoliert.

Die eigentliche Arbeit wird in den Funktionen prepz, prep2 und fdy geleistet, die in folgendem Skript aufgerufen werden:

prep2_1.R

fdy <- function(fn) {
load(paste(fn,".dat",sep=""))
pl <- prepz(complex(real=ip(qrea$hl),imaginary=ip(qrea$vl)))
pr <- prepz(complex(real=ip(qrea$hr),imaginary=ip(qrea$vr)))
save(pl,pr,file=paste(fn,".oz2",sep=""))
prep2(pl,pr)
}
for( fn in names(ausw.liste)) ausw.liste[[fn]]$sakks2 <- fdy(fn)

Zur Optimierung der Performance werden die horizontalen und vertikalen reellen Komponenten jedes Auges zu einer komplexen Zeitreihe zusammengefügt. Evtl. NAs sind nicht erlaubt, daher wird mit Hilfe der Funktion ip interpoliert. Die NAs werden dann mit Hilfe der Liste aus der Vorauswertung rekonstruiert.

Die Zeitreihe z soll auf die doppelte Länge gedehnt werden. Dazu wird die Reihe zunächst so auf die Länge der nächsthöheren 2erpotenz verlängert, daß die Unstetigkeit beseitigt zwischen Ende und Anfang beseitigt wird, die zu unschönen Artefakten bei der Transformierten führt. Folgende Variante wurde implementiert: die Reihe wird spiegelsymmetrisch fortgesetzt, dabei aber exponentiell vermindert in Richtung auf den Mittelwert zwischen erstem und letzten Wert der ursprünglichen Reihe, mit geeigneten Konstanten rn, rn0, rn1:

     
c((z[rn]+z[1])/2+(z[1]-z[rn])/(2*rn0)*1:rn0+(2*z[1]-z[rn0+1-1:rn0])*exp(-12*(rn0+1-1:rn0)/rn0),
   z,
   z[rn]+(z[1]-z[rn])/(2*rn1)*1:rn1+(2*z[rn]-z[rn+1-1:rn1])*exp(-12*(-1+1:rn1)/rn1)))

Das Oversampling wird dadurch erreicht, daß der Fouriertransformierte in ihrer Länge so verdoppelt wird, daß die höchsten Frequenzen zu Null gesetzt werden und die Frequenzen oberhalb der Nyquistfrequenz n4 abgeschwächt werden. Für diesen Übergang wird üblicherweise das Quadrat der Cardinalsinusfunktion sin(x)/x bis zur 1. Nullstelle verwendet:

sinc2 <- (sin(pi/n2*1:n2) *n2/pi / 1:n2 )^2
z.fft.o <- c(z.fft[1:n4],z.fft[n4+1:n2]*sinc2,
  rep(0,2*(n-n3)),
  z.fft[n-n4-n2+1:n2]*rev(sinc2),z.fft[n-n4+1:n4])

Die überabgetastete Zeitreihe wird mit der inversen FFT berechnet:

z.fft.i <- fft(z.fft.o,inv=T) / n

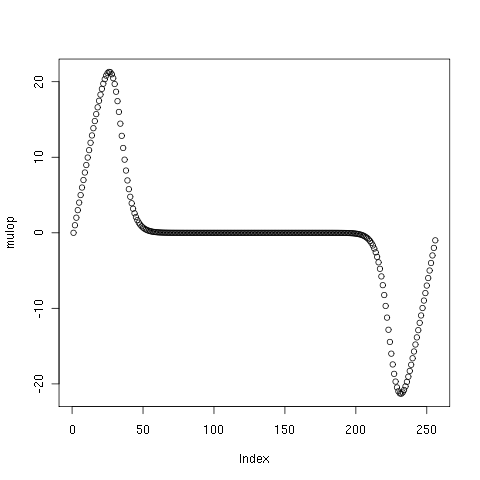
Im Fourierbereich läßt sich auch gleich die Ableitung (Geschwindigkeitsberechnung) vornehmen, indem die Frequenzkomponenten mit dem Frequenzwert multipliziert werden; auch hier wird oberhalb einer geeigneten Grenzfrequenz kontinuierlich abgeschwächt. In R ist zB die logistische Anpaßfunktion SSfpl gut geeignet:

mulop <- c(-1+1:n,-n-1+1:n)
mulop <- mulop * SSfpl(abs(mulop),1,0,n5,n5/8)

Die Funktion liefert eine Liste mit den wesentlichen Konstanten der Zeitreihe, die Fouriertransformierte, die überabgetastete Reihe, ihre 1. Ableitung dz1 sowie noch die mit dg(10) ermittelte Ableitung dz10 zurück.

prepz.R

prepz <- function(z) {
rn <- length(z)
logn <- ceiling(log2(rn+100))
n <- 2^logn
rn0 <- floor((n-rn)/2)
n2 <- floor(n/2)
n4 <- floor(n/4)
n3 <- n2+n4
n5 <- n4
#z0 <- (z[rn]-z[1])
rn1 <- n-rn0-rn
z.fft <- fft(
        c((z[rn]+z[1])/2+(z[1]-z[rn])/(2*rn0)*1:rn0+(2*z[1]-z[rn0+1-1:rn0])*exp(-12*(rn0+1-1:rn0)/rn0),
        z,
        z[rn]+(z[1]-z[rn])/(2*rn1)*1:rn1+(2*z[rn]-z[rn+1-1:rn1])*exp(-12*(-1+1:rn1)/rn1)))
sinc2 <- (sin(pi/n2*1:n2) *n2/pi / 1:n2 )^2
z.fft.o <- c(z.fft[1:n4],z.fft[n4+1:n2]*sinc2,rep(0,2*(n-n3)),z.fft[n-n4-n2+1:n2]*rev(sinc2),z.fft[n-n4+1:n4])
z.fft.i <- fft(z.fft.o,inv=T) / n
mulop <- c(-1+1:n,-n-1+1:n); mulop <- mulop * SSfpl(abs(mulop),1,0,n5,n5/8)
z.fft.d <- fft(z.fft.o*mulop,inv=T) * 1000*pi / n^2
rn <- 2 *rn
rn0 <- 2 *rn0
list( n=n, rn=rn, rn0=rn0, z.fft = z.fft, oz = z.fft.i[rn0+1:rn], dz1 = z.fft.d[rn0+1:rn],
        dz10.h = filter(Re(z.fft.i),dg(10))[rn0+1:rn], dz10.v = filter(Im(z.fft.i),dg(10))[rn0+1:rn])}

Diese Ergebnisse werden in einer Datei mit Endung .oz2 gespeichert (s. Organisation des Skripts prep2.R).

Die in prepz() erzeugten Zeitreihen pl und pr werden zunächst wieder in reelle Zeitreihen in einem Dataframe orea konvertiert:

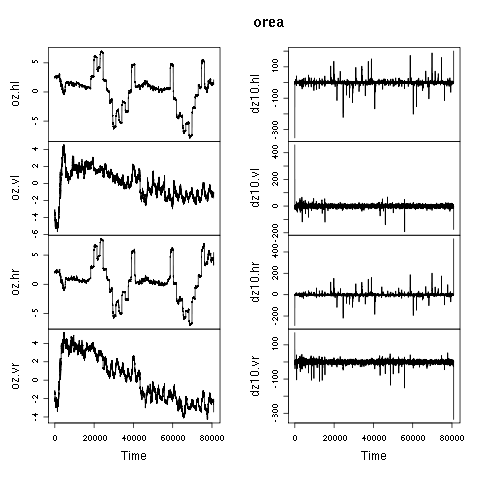
Für die Sakkadenerkennung wird der Betrag der Augengeschwindigkeit nach Pythagoras aus den hor. und vert. Geschwindigkeiten je Auge berechnet.

orea$zl<- sqrt(orea$dz10.hl^2 + orea$dz10.vl^2)
orea$zr<- sqrt(orea$dz10.hr^2 + orea$dz10.vr^2)

Eine Sakkade wird erkannt, wenn das 6fache des Medians überschritten wird. Sakkadenmittelpunkte sind somit alle Maxima des Geschwindigkeitsbetrags oberhalb dieses Limits:

ml <- maxima( orea$zl, limit=6*mzl )      # Sakkadenmitte auf dem lk. Auge

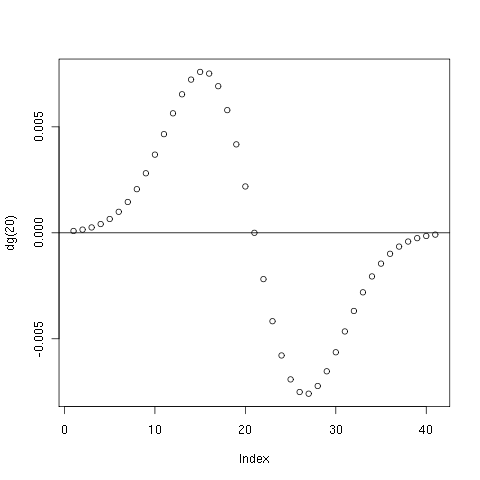
Außerdem werden die Anfangs- und Endzeitpunkte der Sakkaden ermittelt, indem die Augengeschwindigkeit noch einmal mit dg(20) differenziert wird:

z <- filter( orea$zl, dg(20) ); z[is.na(z)] <- 0;
al <- maxima( pmax(0,z), limit=6*median(z[z>0]) )
el <- maxima( pmax(0,-z), limit=6*median(-z[z<0])

Die Listen ml, al und el haben nicht dieselbe Länge, da Artefakte enthalten sind. Eine Bereinigung erfolgt dadurch, daß solche Fälle extrahiert werden, in denen Anfang, Mitte und Ende der Sakkade zeitlich richtig direkt aufeinander folgen:

tr <- data.frame(rbind(cbind(al,1),cbind(ml,2),cbind(el,3)))
colnames(tr) <- c("t","v")
tr <- tr[order(tr$t),]
trx <- (1:length(tr$v))[tr$v==2 &c(0,tr$v[-length(tr$v)])==1 & c(tr$v[-1],0) ==3]

Für alle gefundenen Sakkaden werden die Geschwindigkeiten und Sakkadenweiten ermittelt:

t1l <- tr$t[trx-1]
t2l <- tr$t[trx]
t3l <- tr$t[trx+1]
w.hl <- orea$oz.hl[t3l+1] - orea$oz.hl[t1l-1]
v.hl <- orea$dz10.hl[t2l]
w.vl <- orea$oz.vl[t3l+1] - orea$oz.vl[t1l-1]
v.vl <- orea$dz10.vl[t2l]

Analog wird für das rechte Auge vorgegangen. Die ermittelten Sakkadendaten werden in einer Liste an das aufrufende Skript zurückgegeben.